8.3 Part 2) Convert LDFs from Base Layer

Convert LDFs from base layer to LDFs at any other layer

At this step we should already have \(F_{nj}^B\) selected from the base triangle created above

\[\begin{equation} F_{ij}^X = F_{nj}^B \times \frac{LEV(X;\Phi_{i\infty})\div LEV(B;\Phi_{n\infty})}{LEV(X;\Phi_{ij}) \div LEV(B;\Phi_{nj})} \tag{8.4} \end{equation}\]

  • Without trend, you can basically just take the middle part as the LDFs

    e.g. \(F^B_{nj} = \dfrac{LEV(B; \Phi_{n \infty})}{LEV(B; \Phi_{nj})}\) then it all just cancels out

  • However, we trust the LDF from the analysis of losses limited to \(B\) more and less so with the distribution functions \(\Phi\)

    \(\therefore\) We take the LDF from the limited analysis and scaling from layer \(B\) to \(X\)

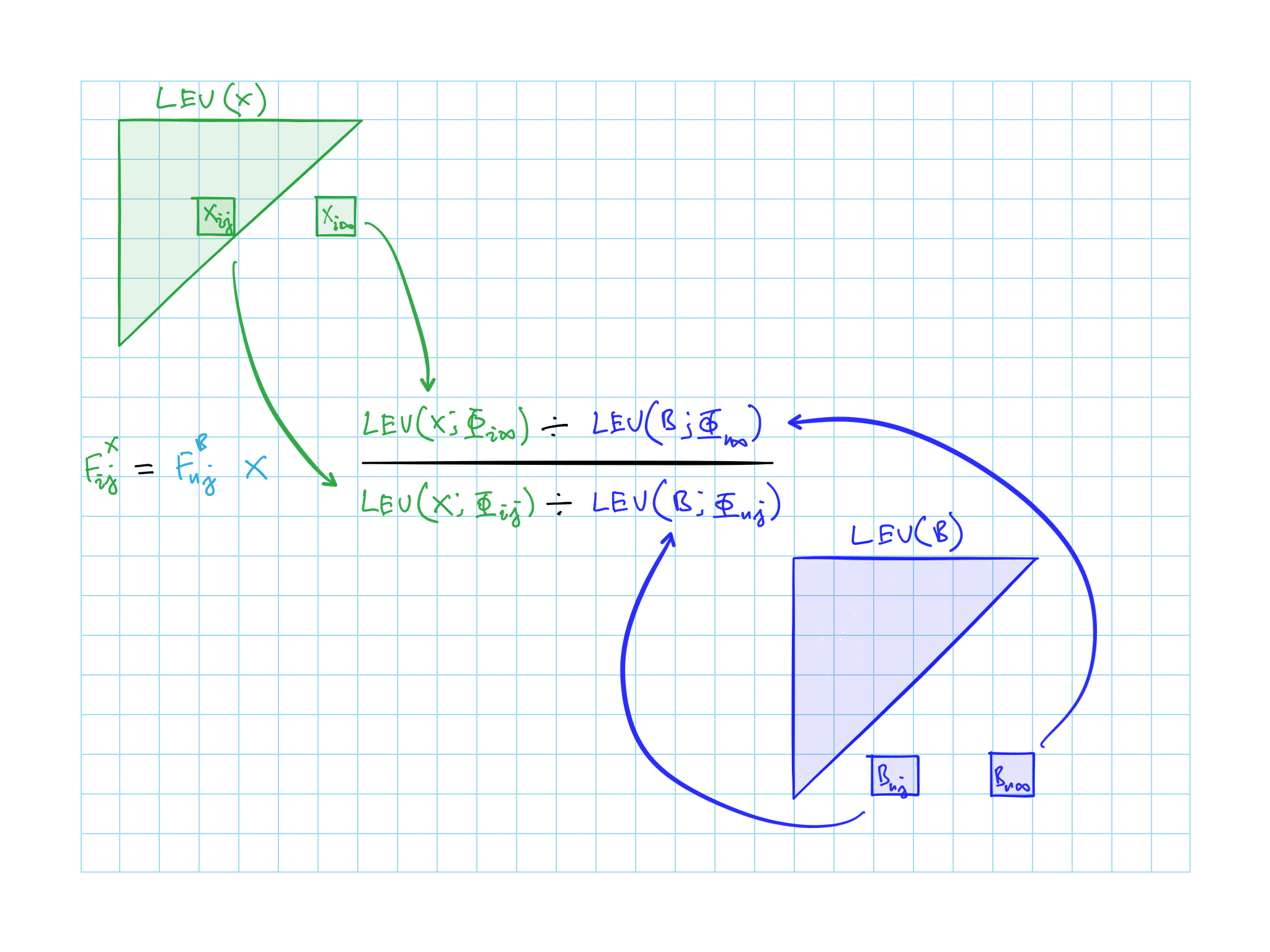
Converting LDFs from base layer to any other layer

Figure 8.1: Converting LDFs from base layer to any other layer

8.3.1 LDFs for Layers from Basic Limits to Policy Limits

\[\begin{equation} F_{ij} = F_{nj}^B \times \frac{ \left[{\color{blue}{LEV(Y;\Phi_{i\infty}) - }} LEV(X;\Phi_{i\infty})\right]\div LEV(B;\Phi_{n\infty})}{ \left[ {\color{blue}{LEV(Y;\Phi_{ij}) - }} LEV(X;\Phi_{ij}) \right] \div LEV(B;\Phi_{nj})} \tag{8.5} \end{equation}\]

\(Y\) here is the policy limits and \(X\) is the basic limits