9.1 Introduction

Paper focus on over-dispersed Poisson (ODP) bootstrap

  • Incremental losses are modeled as ODP random variable

  • Goal is to generate a distribution of possible outcomes

Just FYI, not important for exam

Other papers on bootstrap

  • Statistics: Bradley Efron (1979)

  • Actuarial: England & Verrall (1999; 2002), Pinheiro, et al. (2003), Kirschner, et al. (2008)

Practical motivation for modeling loss distribution

  • Definition of actuarial estimate in ASOP 43 can be based on a first moment from a distribution

    • While ASOP 36 (SAO) focus on deterministic point estimates

  • SEC is looking for more information on reserving risk in the 10-K

  • Rating agencies are building dynamic risk models and welcome actuary input

  • Companies that use dynamic risk models for internal risk management need unpaid claim distributions

  • SII and IFAS are moving towards unpaid claim distribution

Advantages of bootstrap

  • Generates a distribution of the estimate of unpaid claims

  • Can be tailored to statistical features of our data

  • Reflects that loss distn are usually skewed to the right

Disadvantages of bootstrap

  • Takes more time to create, but okay once set up

9.1.1 Stochastic vs Static Model

ODP bootstrap is a specific form of GLM

Benefit of GLM: It can be specifically tailored to the statistical features found in the data

  • Contrast with algorithms that force the data to be fit to a static model (fig. 9.1)
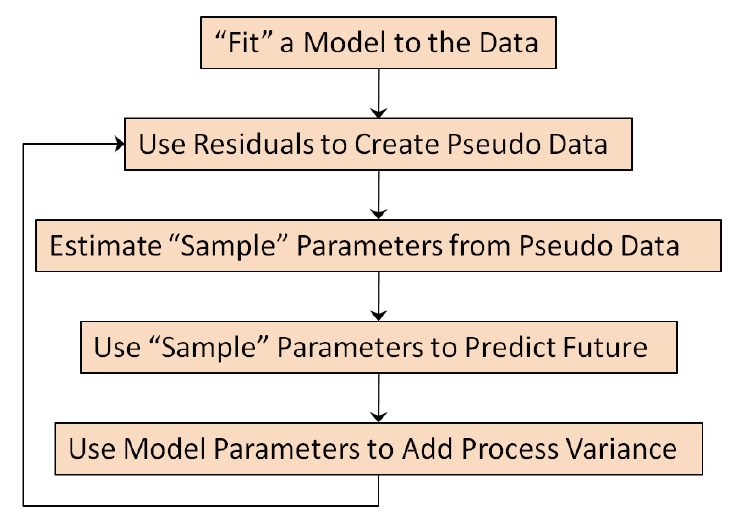
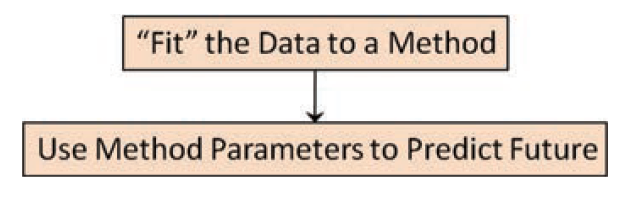
Stochastic vs Static Model DiagramStochastic vs Static Model Diagram

Figure 9.1: Stochastic vs Static Model Diagram

Just FYI, not important for exam

Some authors define a model as having a defined structure and error distribution, so under this more restrictive definition bootstrapping would be considered to be a method or algorithm

However, using a less restrictive definition of a model as an algorithm that produces a distribution, bootstrapping would be defined as a model