11.3 Testing Procedure

We are testing the process of each method and not the results of any one distribution generated from the method

  • Since there’s only 1 actual outcome for each triangle we test

  • Focus on the process (the different methods) that gives us the distribution

  • Compare the predicted percentiles (from the methods) against the expected percentile

  • Typically we can compare distributions by comparing the density function, but we can not in this case because 1) We have a small data sets (50 points) 2) Each data point comes from a different distribution

Testing Procedure

  • Given \(N\) triangles and their actual outcome in 10 years

  • Generate \(N\) sets of distribution (from the \(N\) triangles using one of the methods) and determine the predicted percentile \(p_i\) based on the predicted distribution

    • i.e. see where the actual outcome lands on our predicted distribution

  • The distribution of the \(N\) predicted percentiles \(p_i\) should follow a uniform distribution if the model is accurate, so we rank them to form \(\{p_i\}\)

\[\{p_i\} = \{p_1,...,p_n\}\]

  • The expected percentiles \(\{e_i\}\) should run from \(\frac{1}{n+1}\) to \(\frac{n}{n+1}\)

\[\{e_i\} = \left\{ \dfrac{1}{n+1}, \dfrac{2}{n+1},...,\dfrac{n}{n+1} \right\}\]

11.3.1 Kolmogorov-Smirnov Test

For the KS test we’ll compare \(\{ p_i \}\) with \(\{ f_i \}\)

\[\begin{equation} \{f_i\} = \left\{ \dfrac{1}{n}, \dfrac{2}{n},...,\dfrac{n}{n} \right\} \tag{11.1} \end{equation}\]

\(H_0\): Distribution of \(p_i\) is uniform

Test statistics for maximum difference between the predicted and expected percentiles

\[\begin{equation} D = \max \limits_i \mid p_i - e_i \mid \tag{11.2} \end{equation}\]

Reject \(H_0\) @5% confidence level if:

\[\begin{equation} D > \dfrac{136}{\sqrt{n}}\% \tag{11.3} \end{equation}\]
  • i.e. For \(n = 50\) \(\Rightarrow\) 19.2%; \(n=200\) \(\Rightarrow\) 9.6%

Example

Table 11.1: Kolmogorov-Smirnov test example
\(f_i\) \(p_i\) \(abs\{ p_i - f_i \}\)
(1) (2) (3)

  1. Col (1): \(\{f_i\} = \left\{ \dfrac{1}{n},...,\dfrac{n}{n}\right\}\)

  2. Col (2): \(\{p_i\}\) = \(p_i\) from each realization of the triangles sorted in ascending order

  3. Col(3) = Absolute difference between the first two columns

  4. \(D\) is the maximum value from column (3)

  5. Compare \(D\) with \(\dfrac{136}{\sqrt{N}}\)

    If \(D\) is less than the critical value we do not reject the \(H_0\) that \(\{ p_i \}\) is uniform

Remark. Technically based on Klugman you test against both:

\[\{f^+_i\} = \left\{ \dfrac{1}{n}, \dfrac{2}{n},...,\dfrac{n}{n} \right\}\]

and

\[\{f^-_i\} = \left\{ \dfrac{0}{n}, \dfrac{2}{1},...,\dfrac{n-1}{n} \right\}\]

Alternatively, we can use Anderson-Darling test that focuses on the tail

  • But it failed all the models therefore we do not use it as it does not help in model comparison

11.3.2 p-p Plot

We plot the \(p-p\) plot with \(e_i\) vs \(p_i\) to diagnosis

  • Dark blueline is what is expected from uniform distribution

  • Light blueline is the critical value for a given \(n\) from the KS test above

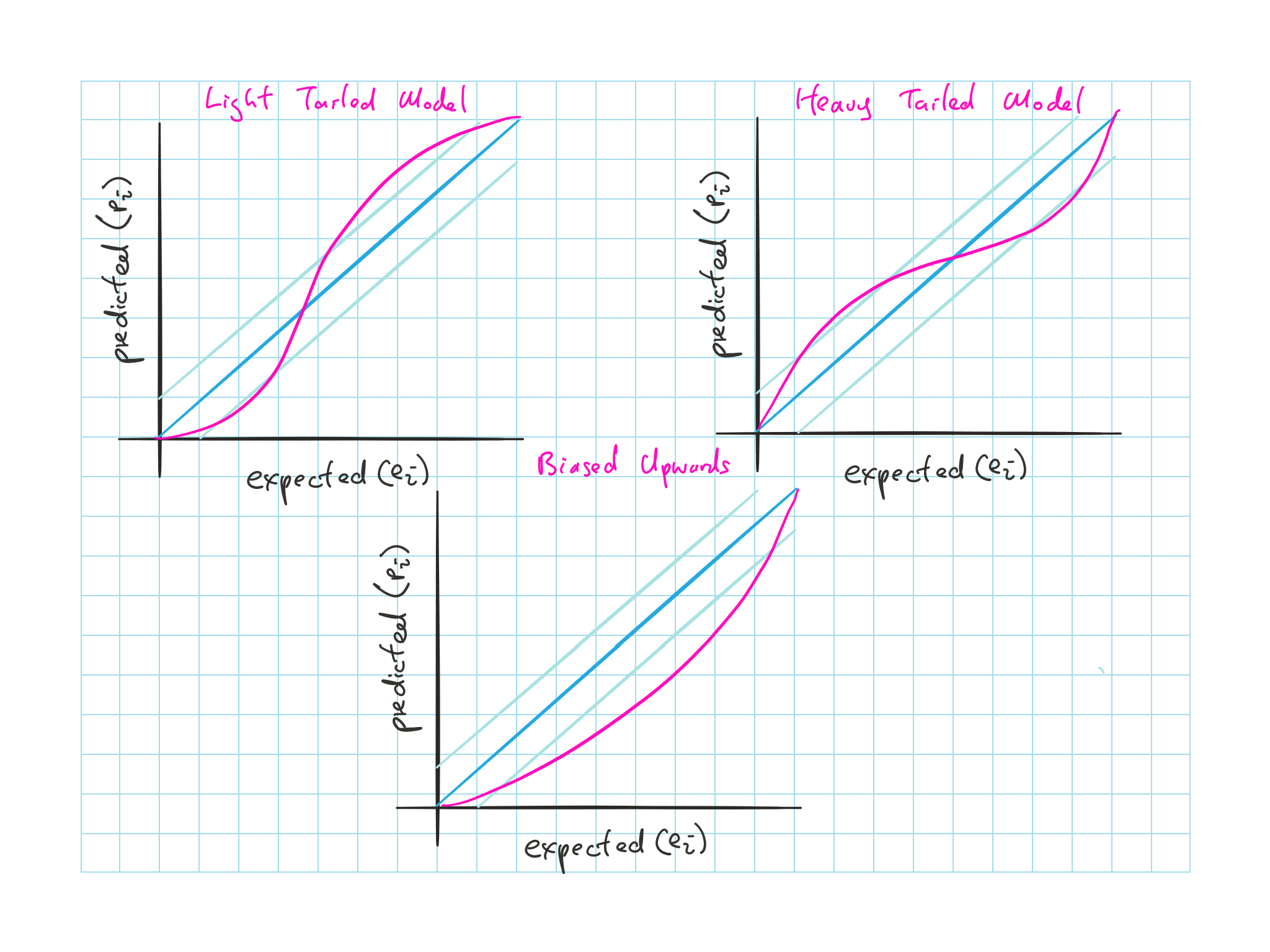
p-p plot

Figure 11.1: p-p plot

  • Model is too light tailed: Shallow slope near corner and steep in the middle

  • Model is too heavy tailed: Steep slope near corner and shallow in the middle

  • Model is biased upwards: Bow down

    • Biased upwards: predicted mean > true mean while the s.d. is correct

  • If we look at lognormal data fitted to normal, we’ll see a mix of light and heavy tailed model

    • i.e. The right tail will be too light so we’ll see a shallow slope in the right and the left tail will be too light so we’ll see a steep slope at the left

11.3.3 Percentile Histogram

We plot a (flipped) histogram

  • y-axis being the predicted percentile

  • x-axis is the frequency

  • Bins with width 0.1 (so 10 bins)

  • Vertical blue line represent the expected frequency based on uniform \(\{e_i\}\)

    • Expected frequency = \(\dfrac{\text{# of points}}{\text{# of bins}}\)= \(\dfrac{n}{10}\)
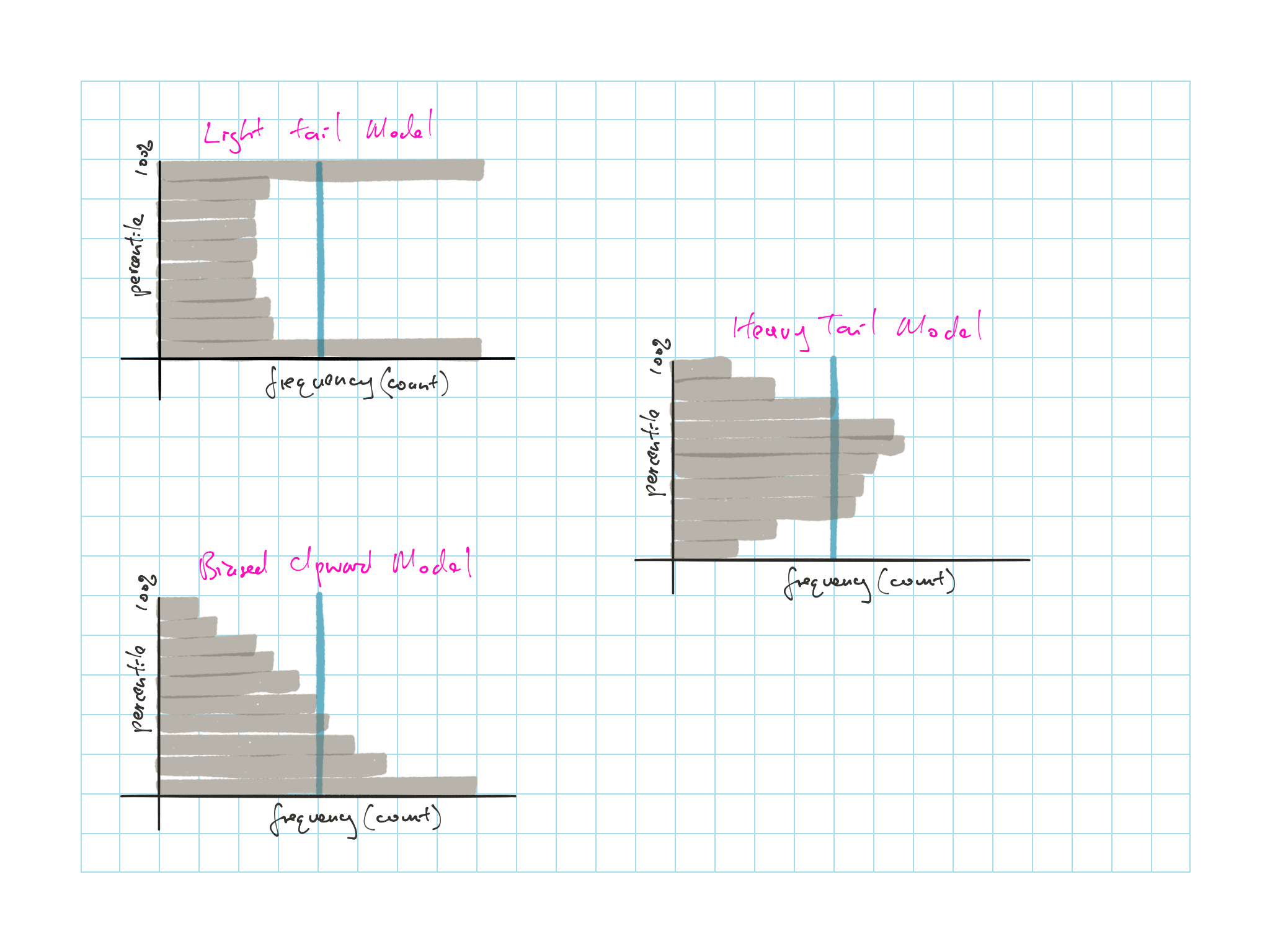
Percentile Histogram

Figure 11.2: Percentile Histogram